Modelling of water ecosystems respondent to changes in external conditions

Viktor V. Boulion* & Lars Hekanson**

* Zoological Institute, Russian Academy of Sciences, Universitetskaya nab., 1, St. Petersburg, 199034, Russia
**Uppsala University, Departament of Earth Sciences, Villav. 16, Uppsala, 752 36, Sweden

Prediction of matter flow intensity and water trophic state is the major direction of modern hydroecology. The development of prediction bases is related to the solution of the following tasks.

The creation of a database for a large number of water bodies of different regions and for as large number of variables as possible. For this purpose we have collected material for lakes of the humic zone (northwestern part of Russia and western Europe), the arid zone (Trans-baikalia, Mongolia), the mountain region (East Pamir) and high latitudes (Kola Peninsula, the of Franz Josef Land archipelago). Besides, exten-sive literature is involved (Boulion, 1994, 1997; Håkanson & Peters, 1995; Håkanson, 1999).
Quantitative description of regular relations between various hydrological, physical-chemical and hydrobiological parameters. Such parameters include average depth of water bodies, water retention time, spe-cific catchment area, coefficient of phosphorus export from catchment, input of precipitation phosphorus, latitude, altitude and continentality, colour and transparency of water, temperature, contents of chlorophyll, particulate organic matter, total and particulate phosphorus, photosynthesis rate, annual primary production, fish yield, etc.
The listed parameters are important for integrated assessment of lake ecosystem state (degree of eutrophication, acidification, etc.). They are conditionally subdivided into two groups: x-variables (independent, or driven) and y-variables (dependent, or target). The first group includes practically all hydrological, morphometric and geographical factors, the so-called 'map parameters' (Håkanson, 1996; Håkanson & Carlsson, 1998). Among "target" variables the annual primary production and the fish yield are of the greatest practical interest. Water transparency, contents of chlorophyll, particulate organic matter, total and particulate phosphorus, photosynthesis rate can act in a chain of interrelations both as x-variables and as y -variables depending on the tasks.

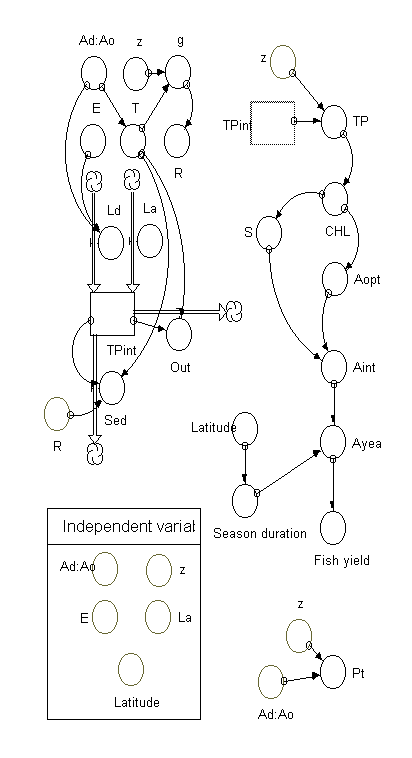
Fig. 1. Simple model for prediction of the intermediate (total phosphorus, chlorophyll, Secchi depth, water colour, photosynthesis rate) and target dependent variables (annual primary production, fish yield) on the basis of independent (or driven) variables (specific catchment area, coefficient of total phosphorus export, precipitation of total phosphorus, latitude). See symbols in Appendix

Since the above listed parameters are interconnected (directly or indirectly), they form the basis for predicted models. We have made steps towards the development of two types of models. The model of the first type is holistic, because it reflects a largely external aspect of ecosystem functioning and it is intended for prediction of target parameters (e.g. the primary production of plankton and the fish yield) under different values of the following x-variables: average depth of water bodies, water retention time, specific catchment area, coefficient of phosphorus export from catchment and latitude (see Fig. 1-3 and Appendix). The model of the second type is characterized by reductionistic direction because it describes, according to our knowledge, in great detail the matter flows within the ecosystem, i.e. the flows between plankton components (phytoplankton, zooplankton, bacteria and protozoans), detritus and dissolved organic matter. The given model allows to reconstruct the seasonal dynamics of biomass of the major plankton groups and the rate of carbon flows under the influence of the abiotic factors, i.e. concentration of total phosphorus, water temperature, etc.

The studies were carried out with financial support of INTAS (Project 306) and the Russian Foundation for Basic Research (grants 99-04-49614 and 00-15-97825).

Fig. 2. Modelling of the total phosphorus content (1) and annual primary production (2) in a lake located at 60o N at medium other condition: specific catchment area (Ad : Ao) = 10, mean depth (z) = 5 m, coefficient of total phosphorus export from catchment (E) and total phosphorus precipitation (La) = 0.020 ± 0.005 g · m -2 · yr -1 (see Fig. 1 and Appendix). The dynamic equilibrium in total phosphorus content and fish yield is achieved after 4 years.

Trophic status of lake is close to that for mesotrophic water bodies

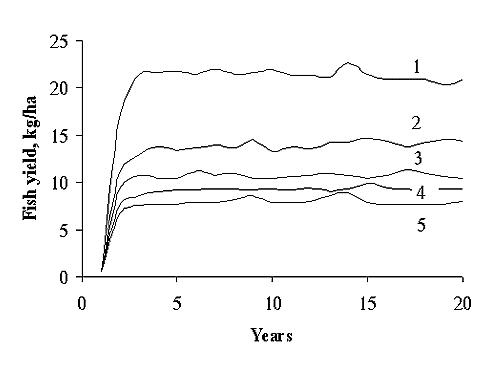
Fig. 3. Dependence the annual fish yield on mean depth (z): 1– 2 m; 2 – 4 m; 3 – 6 m; 4 – 8 m; 5 – 10 m. Latitude = 60^o N; A_d : A_o = 10; E = 0.020 ± 0.005 g P · m ^-2 · yr ^-1; L_a = 0.020 ± 0.005 g P · m ^-2 · yr ^-1. See symbols in Appendix. The relationships between variables are indicated in Fig. 1 and Appendix

Appendix

The list of the equations used in the model (see Fig. 1) meant for prediction of the annual primary production and fish yield in lake ecosystems

BOX

TPint(t) = TPint(t – dt) + (La + Ld – Out – Sed) * dt INIT TPint = 0

DOCUMENT: Total phosphorus contents in lake, g 10.0pt">·m^-2.

INFLOWS:

La = RANDOM(0.015,0.025)

DOCUMENT: Precipitation phosphorus load, g · m^-2· yr^-1.

It is assumed that La = 0.020 g · m ^-2· yr^-1and CV = 25%. Ld = Ad:Ao*E

DOCUMENT: Terrestrial phosphorus load, g·m^-2·yr^-1.

OUTWLOWS:

Out = TPint/T

DOCUMENT: Phosphorus outflow from lake, g · m^-2· yr^-1.

Sed = TPint*R/T

DOCUMENT: Phosphorus sedimentation in lake, g · m^-2· yr^-1.

VARIABLES:

Ad : Ao = 10

DOCUMENT: Specific catchment area, i.e. the ratio of catchment area to lake area (km²/km²).

Aint = 0.64*(Aopt*S)^1.069

DOCUMENT: Mean-summer areal primary production, mg C · m^-2· day^-1 (Boulion, 1997).

Aopt = 30.6*CHL^0.927

DOCUMENT: Mean-summer photosynthesis rate at “optimal” depth, mg C · m^-3· day^-1 (Boulion, 1997).

Ayear = Season_duration*Aint/100

DOCUMENT: Annual primary production, kcal · m ^-2.

CHL = 0.01+0.073*TP^1.451

DOCUMENT: Mean-summer chlorophyll concentration in a lake (according to the equation of Dillon and Rigler, 1974), mgm^-3.

To avoid unrealistically low chlorophyll concentrations the constant 0.01 as minimum concentration of the chlorophyll in natural waters is added in the equation.

E = RANDOM(0.015,0.025)

DOCUMENT: Coefficient of phosphorus export in lake, g · m^-2· yr ^-1.

It is assumed that E = 0.020 g · m^-2· yr ^-1and CV = 25%.

Fish_yield = 0.013*Ayear^0.996

DOCUMENT: Fish yield, kg · ha^-1 (Boulion, 1997).

g = z/T

DOCUMENT: Hydraulic load, m · yr ^-1.

Latitude = 60

DOCUMENT: Latitude in ^oN.

Pt = 25.3*(Ad : Ao/z)^0.639

DOCUMENT: Water colour in lake (according to Boulion, 1995).

R = 0.201*EXP(-0.0425*g)+0.574*EXP(-0.00949*g)

DOCUMENT: Coefficient of phosphorus retention in lake, dimensionless value (Ostrofsky, 1978).

S = 6.01*CHL^ (-0.517)

DOCUMENT: Mean-summer water transparency (Secchi depth) in lake, m (Boulion, 1997).

Season_duration = -0.058*Latitude^2+0.549*Latitude+365

DOCUMENT: Season duration, days.

T = 1/(0.036*Ad:Ao^1.316)

DOCUMENT: Water retention time, years.

According to Kitaev (1984).

TP = 1000*TPint/z

DOCUMENT: Total phosphorus concentration in lake, mg · m^-3.

z = 5

DOCUMENT: Mean depth, m.

References

Boulion, V.V. 1994. Zakonomernosti pervichnoi produktsii v limnicheskikh ekosistemakh [The regularity of primary production in limnetcic ecosystems]. St.-Petersburg, Nauka. 222 pp. (In Russian.)

Boulion, V.V. 1995. Reconstruction of phosphorus budget of two Karelian lakes of different type. Hydrobiol. Zh. 31: 3-14. (In Russian.)

Boulion, V.V. 1997. Regularities of the plankton primary production and their importance for the control and prediction of a trophic condition in water ecosystems. Biol. vnutrenn. Vod 1: 13-22. (In Russian.)

Dillon, P.J. & F.H. Rigler. 1974. The phosphorus-chlorophyll relationship in lakes. Limnol. Oceanogr. 19: 767-773.

Hekanson, L. 1996. A new, simple, general technique to predict seasonal variability of rive discharge and lake temperature for lake ecosystem models. Ecol. Modelling 88: 157-181.

Hekanson, L. 1999. Water pollution - methods and criteria to rank, model and remediate chemical threats to aquatic ecosystems. Leiden, Backhuys Publ. 299 pp.

Hekanson, L. & L. Carlsson. 1998. Fish farming in lakes and acceptable total phosphorus loads: calibrations, simulations and predictions using the LEEDS model in Lake Southen Bullaren, Sweden. Aquatic Ecosystem Health and Management 1: 1-24.

Hekanson, L. & R.H. Peters. 1995. Predictive limnology. Methods for predictive modelling. Amsterdam, SPB Academic Publ. 464 pp.

Kitaev, S.P. 1984. Ekologicheskie osnovy bioproduktivnosti ozer raznykh prirodnykh zon [Ecological principles of productivity of the lake of different natural zones]. Moskva, Nauka. 207 pp. (In Russian.)

Ostrofsky, M.L. 1978. Modification of phosphorus retention models for use with lakes with low areal water loading. J. Fish. Res. Bd Can. 35: 1532-1536.